离散弱形式

这篇文章继续我们关于弱配方的博客系列。在里面上一篇文章，我们在Comsol多物理软件中实现并解决了一个模范弱形式。结果通过简单的物理参数验证。今天，我们将开始进行幕后观察方程式如何被数字化和解决。

我们的简单示例

回想我们在没有热源的稳态下的一维热传递的简单示例，温度t是位置的函数X在由间隔定义的域中1 \ le x \ le 5。在边界条件下，即将上流通量应在左边界处为2（x = 1）并且温度应为右边界9（x = 5），弱形式读取：

（1）

现在，我们尝试找到一种方法来数值求解该方程。

基础功能

解决方程。（1）数字上，我们首先将域分开1 \ le x \ le 5分为四个均匀间隔的子媒体，或网格元素，被五个节点点x = 1，2，\ cdots，5。然后，我们可以定义一组基础函数，或形状功能，，，，\ psi_ {1l}（x），\ psi_ {1r}（x），\ psi_ {2l}（x），\ psi_ {2r}（x）（x），\ cdots，\ psi_ {4r {4r}（x）（x），如下图所示，每个网格元素中有两个形状函数，以实线和虚线表示。

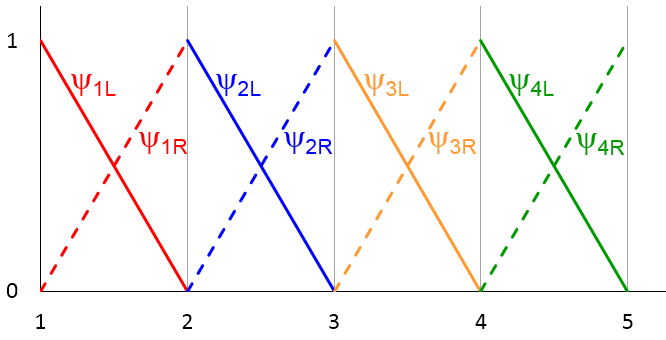
例如，在第一个元素中（1 \ le x \ le 2）， 我们有

（2）

我们观察到每个形状函数都是一个简单的线性函数，范围从网格元素内的0到1，并且在该网格元素之外消失。

注意：当然，comsol多物理允许形成具有高阶多项式的形状函数，而不仅仅是线性函数。线性形状函数的选择是为了视觉清晰度。

有了这组形状功能，我们可以近似域中定义的任何任意功能1 \ le x \ le 5通过简单的线性组合：

（3）

在哪里a_ {1l}，a_ {1r}，a_ {2l}，a_ {2r}，\ cdots是一些恒定系数，一个用于每个形状函数。在下图中，任意函数u（x）由黑色曲线表示。青色曲线表示形状函数的叠加近似（3）。等式右侧的每个术语。（3）使用与上图相同的颜色和线样式绘制。

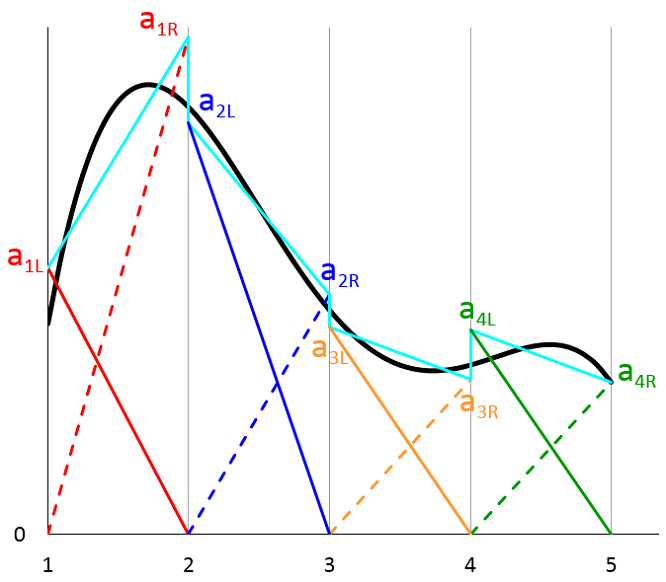
我们看到，通常，在相邻的网格元素之间的边界上，近似值（由青色曲线表示）可能是不连续的。实际上，许多物理系统，包括我们简单的热传导示例，都将具有连续的解决方案。因此，大多数物理接口的默认形状函数是拉格朗日元素，其中形状函数系数受到约束，因此该解在相邻元素之间的边界之间是连续的。在这种情况下，简化了近似值，如下图所示

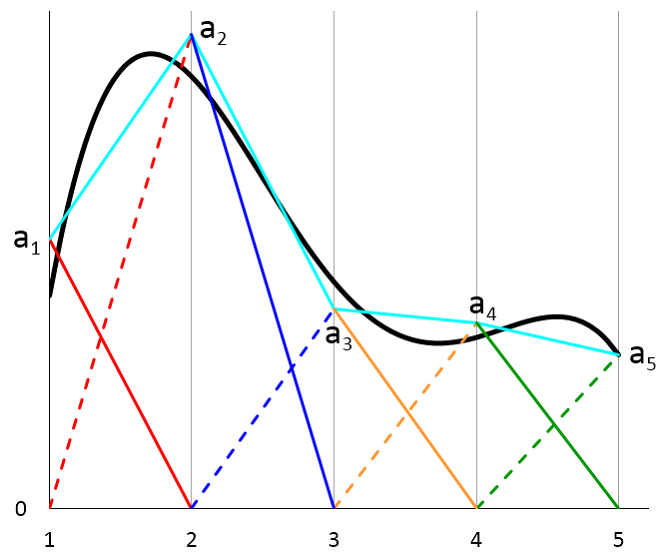
如果通过将系数设置在网格边界的每一侧，则使蓝色曲线连续。a_ {1r} = a_ {2l}，a_ {2r} = a_ {3l}，a_ {3r} = a__ {4l}。我们还重命名为简洁的系数：

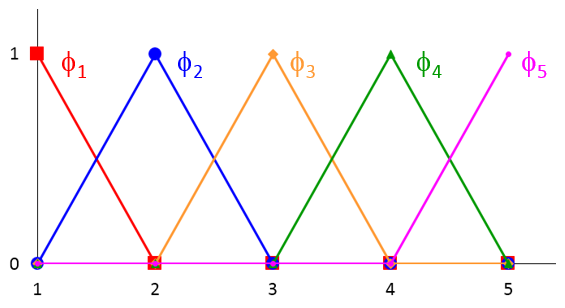
我们看到，连续性条件需要成对的形状函数才能共享相同的系数。（3），现在可以通过将这些形状函数组合到新的基础函数中来简化它ϕ1（x），ϕ2（x），⋯，ϕ5（x），每个函数都位于一个淋巴结周围：

（4）

如下图所示，每个新的基础函数本质上都是一个三角形的，分段线性函数，以围绕节点点为中心。它的值在与节点点相邻的网格元素中的1到0之间变化，并且在其他任何地方都消失。

如上所述，通过选择一组新的基础函数，我们将解决方案限制为在相邻的网格元素之间的边界上是连续的。大多数物理系统都满足这种连续性约束，包括我们在此处简单的传热示例。

现在，有了这组新的基础函数，近似（3）被简化为

（5）

在下图中，任意函数u（x）由黑色曲线表示。青色曲线代表新基函数的叠加的近似值。等式右侧的每个术语。（5）使用与上图相同的配色方案绘制。

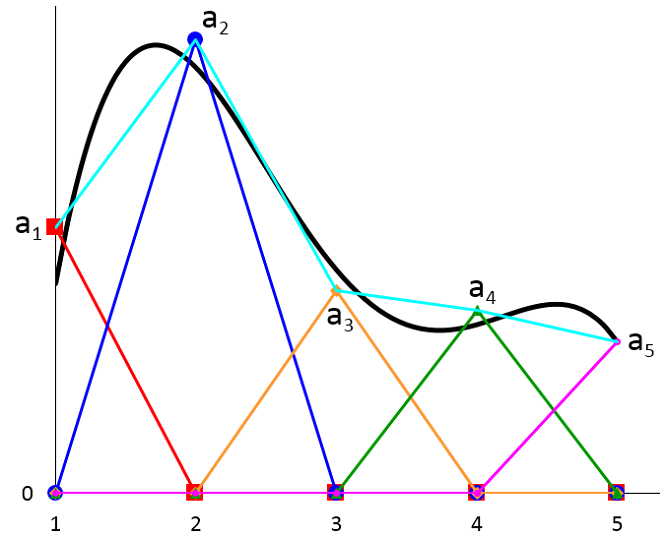
顺便说一句，如果黑色曲线代表了某些真实建模问题的精确解决方案，那么由于网格的粗糙性，我们看到近似值不是很好。同样，总体上，节点值A_1，A_2，\ CDOTS不需要躺在精确溶液上，除非将一个溶液约束到已知的解决方案值（如图所示A_5作为上图中的一个例子）。我们在这里看到的黑色和青色曲线之间的差异表示解决方案的离散误差。在2D和3D模型中，几何学也将存在离散化误差。在我的同事沃尔特·弗莱（Walter Frei）有关网格划分注意事项的博客文章，两种类型的错误将详细讨论。由于这些潜在错误，网状细化研究对于确保建模结果的准确性是必要的。

我们注意到等式给出的近似值。（5）（青色曲线）是分段线性的。因此，不可能通过数值评估其第二个衍生物。正如我们之前提到的，弱公式通过减少方程式中的分化顺序来提供数值益处。在这种情况下，仅需要第一个衍生物，并且可以很容易地对其进行数字评估。在未来的博客条目中，我们将讨论材料属性中不连续性的示例，该示例也从差异的差异顺序中受益。

分两个步骤离散弱形式

随着上面定义的新基集函数集，我们开始离散弱形式方程（1）分两个步骤。首先，温度函数，t（x），可以以与等式中相同的方式来近似基集函数。（5）：

（6）

在哪里A_1，A_2，\ CDOTS，A_5是要确定的未知系数。

代替表达t（x）（6）进入弱形式（1）， 我们获得

（7）

右边界的温度x = 5，，，，T_2，已使用该表达式评估（6）以及基本函数本地化的事实，仅导致一个术语，a_5 \ phi_5（x = 5）= a_5，贡献t（x = 5）。

我们看到，弱形式方程的离散版本中有六个未知数（7）：五个系数A_1，A_2，\ CDOTS，A_5还有一个磁通量\ lambda_2在正确的边界。习惯称未知数为自由程度。例如，我们在这里说（离散的）问题具有“六个自由度”。

要解决这六个未知数，我们需要六个方程式。这导致了离散化的第二步。回想一下我们第一篇博客文章测试函数的作用是在本地采样方程，以限制域内各地的解决方案。现在我们已经有了一组本地化功能，我们的基础功能\ phi_1，\ cdots，\ phi_5，因此我们可以将它们替换为测试功能\ tilde {t}在等式中。（7）要获得我们需要的六个方程式。

这是一张表明将为我们生成六个方程式的六个替代的表：

\ tilde {t}（x）	\ tilde {\ lambda} _2
\ phi_1（x）	0
\ phi_2（x）	0
\ phi_3（x）	0
\ phi_4（x）	0
\ phi_5（x）	0
0	1

由于每个基础函数都是本地化的，因此每个替换都会产生一个少数术语的方程式。例如，第一个替代给出

我们注意到这一点\ phi_1仅与自己有非平地重叠，并且\ phi_2。因此，左侧只有前两个项是非零的。还，\ phi_1位于左边界附近（x = 1），因此只有右侧的第一项保留。现在的方程式变成

（8）

我们在左侧评估了确定积分的地方：

并使用的定义\ phi_1在右手侧：\ phi_1（x = 1）= 1。

同样，上表中列出的其余五个替换产生了以下方程：

（9）

现在，我们有六个未知数的方程式，很简单地验证该解决方案是否与上一篇文章中使用comsol多物理软件获得的内容相匹配。例如，最后一个方程立即给我们A_5 = 9，并使用表达式（6）对于温度，我们在右边界中获得其值：

这与固定边界条件一致，即温度应在右边界处为9。也很容易看到它是与测试功能相关的术语\ tilde {\ lambda} _2这引起了方程式（0 = A_5 -9），正如我们所期望的。

矩阵表示

编写离散的方程式很方便（在我们的简单示例中，有六个方程式（8）和（9））在矩阵和向量方面：

（10）

左侧的矩阵通常称为刚度矩阵右边的向量称为负载向量，由于该技术在结构力学中的应用。

我们注意到有关此矩阵方程的两个有趣的事实。首先，矩阵中有很多零（所谓的疏矩阵）。在一个实用模型中，与这里的四个元素相比，网格元素要多得多，我们可以设想矩阵中的大多数元素将为零。这是选择局部形状函数的直接好处，并且将自己提供给非常有效的数值方法来求解方程系统。

第二，拉格朗日乘数\ lambda_2仅出现在一个方程中（矩阵的最后一列只有一个非零元素）。其余五个方程仅涉及五个未知系数A_1，A_2，\ CDOTS，A_5。因此，我们可以选择解决A_1，A_2，\ CDOTS，A_5使用五个方程式，无需解决\ lambda_2。正如我们在先前的条目通常，可以选择不解决Lagrange乘数以获得计算速度。

摘要和下一个主题，薄弱的形式系列

今天，我们使用我们的简单示例回顾了离散弱形方程的基本程序。我们通过两个步骤利用了一组局部形状功能：

1. 以它们为基础来近似真实的解决方案
2. 将它们一个接一个地替换为弱形式方程以获得离散的方程系统

所得的矩阵方程稀疏，可以使用计算机有效地求解。

在上一篇博客文章中，当我们使用COMSOL多物理学实现弱形式方程时，离散化是在引擎盖下完成的，而无需用户的帮助。接下来，我们将向您展示如何检查刚度矩阵和负载向量，以及如何选择解决或不解决 - 通过使用该Lagrange乘法器弱形式PDE软件中的接口。