如何在comsolMultiphysics®中建模大型粘弹性

许多聚合物和生物组织都表现出粘弹性变形，即使载荷在时间上是恒定的，也具有时间依赖性响应。线性粘弹性是一个常见的近似值，其中应力依赖于应变和应变速率。我们通常假设变形的粘性部分是不可压缩的，因此体积变形纯粹是弹性。与ComsolMultiphysics®5.2A一样，除线性粘弹性外，还可以对大型粘弹性进行建模。请参阅如何在生物医学应用中使用此材料模型。

动脉的力学

动脉是血管，在整个体内携带含氧血液。它们是由Intima组成的分层结构，外部层上有媒体和Adventitia（也称为Externa）。媒体和院子是主要负责健康动脉机械行为的层。

这两个层都是由胶原性软组织组成的，这些软组织表现出明显的应变僵硬行为。由于胶原蛋白纤维家族，每层具有各向异性特性。这意味着这些纤维增强的结构使血管能够经历大型菌株。

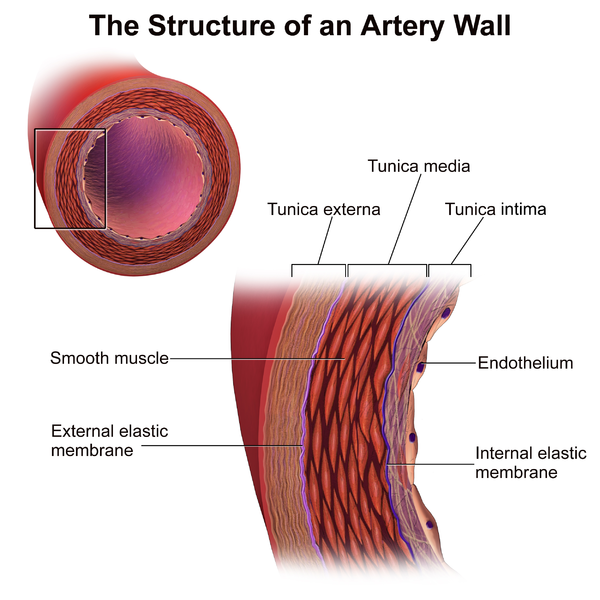
动脉墙的结构。Bruceblaus的图像 - 自己的作品。获得许可CC由3.0， 通过Wikimedia Commons。

一个可靠的动脉壁力学本构模型对于研究年龄和疾病以及设计假体引起的动脉系统的变化至关重要（其他用途）（参考。3）。Holzapfel-Gasser-Ogden（HGO）本构模型（参考。2）捕获上述各向异性机械响应，在切除动脉的实验实验中也观察到了这一点。实验室中的典型实验测量了轴向拉伸和内部血压组合的动脉切片的响应，数值示例试图匹配此数据以更好地了解其力学。

大型粘弹性背后的理论

正如鲍尔指出的那样固体的应用力学：“有限应变粘弹性不如有限菌株可塑性，并且存在许多不同的配方。”在Comsol Multiphysics版本5.2a中，我们实施了大型粘弹性的Holzapfel模型（参考。1，，，，参考。3），非常适合与Comsol®软件中可用的任何预定义的超弹性材料模型相结合。

作者提出了一个广义的麦克斯韦模型，基于应变能密度分解为体积和等距贡献

这里，C代表正确的cauchy绿色变形张量和\ bar {c}代表其等距对应物。与非平衡状态相关的自由能，\ psi_m，是等距右cauchy-green张量的函数\ bar {c}和内部应变样变量\ gamma_m（（参考。1，，，，参考。3）。

纯弹性分支中的应变能通常用上标表示\ infty表示长期平衡（ASt \ rightarrow \ infty）。

然后，Holzapfel在超弹性和粘弹性分支中衍生出第二Piola-Kirchoff应力的表达

并从热力学考虑上定义辅助应力张量

然后，第二次Piola-Kirchoff应力（超弹性和粘弹性分支）由

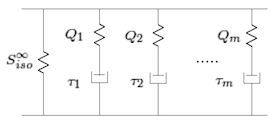
大型粘弹性中广义的麦克斯韦模型的第二piola-kirchoff应力的示意图。

通过求解速率方程式给出了粘弹性分支中应力的演变

在哪里\ tau_m是分支的放松时间，{S} _ {ISO，M}是相应的第二piola-kirchoff应力张量。

Holzapfel还假设应该存在与每个分支上弹簧相关的等速应变能密度，w_ {iso，m}（\ bar {c}）， 所以

Holzapfel形式主义的主要假设是，每个分支的等距应变能取决于主超弹性分支的相位应变能

在这里，无量纲系数\ beta_m> 0被称为应变能量因子。

然后，每个分支的第二个piola-kirchoff应力变成

而解决的速度变成了

所有超弹性材料都可以使用Comsol多物理的5.2a版本中的麦克斯韦粘弹性模型，并且还包含与线性粘弹性实现的热效应的相同选项。

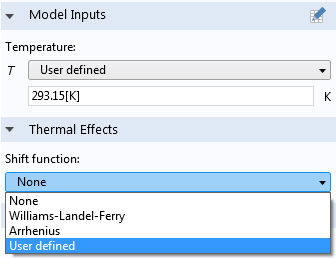
使用用户定义的选项，您可以忽略热效果，使用预定义的William-Landel-Ferry或Arrhenius Shift功能，或定义自己的移位功能。

让我们看一下如何将大型粘弹性应用于生物力学建模。

在COMSOL多物理学中对大型粘弹性进行建模

为了模拟轴向应力突然变化后动脉壁的行为，我们需要使用超维斯弹性材料模型，该模型超出了HGO材料模型。

看一下动脉壁力学教程模型，以获取有关如何设置各向异性超弹性材料的更多详细信息。

首先，让我们在此特定材料模型中添加粘弹性行为。如所述参考。3，添加到HGO模型中的五个分支的广义麦克斯韦模型适合模拟范围从1 ms到10秒的放松时间。该模型适用于定量代表动脉圆周段的粘弹性响应（参考。3）。为此，我们右键单击超弹性材料节点并添加一个粘弹性节点（我们还可以将其与热膨胀或其他效果相结合）。

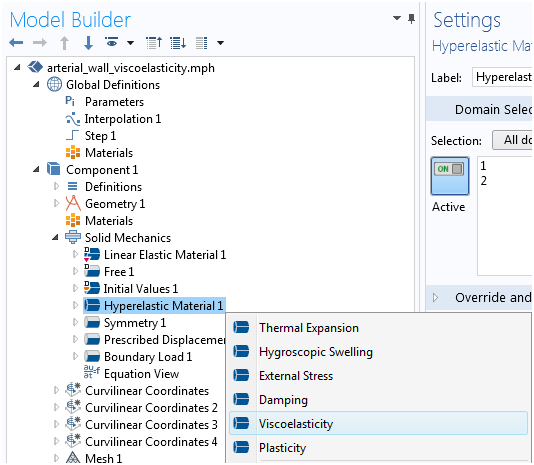
默认情况下，我们将获得一个带有一个分支的广义麦克斯韦模型。但是，我们还可以使用标准的线性固体（SLS）模型或开尔文 - Voigt粘弹性模型。

然后，我们添加了五个分支，其中包括相应的能量因子和放松时间（如（参考。3）。我们能够从文本文件中检索（并保存）此类参数。

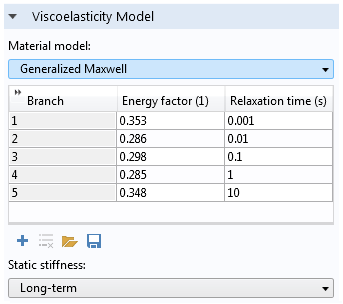
在用五个粘弹性分支翻新HGO高弹性材料后，我们可以模拟在恒定的轴向应变四分钟时在动脉截面中发生的情况。

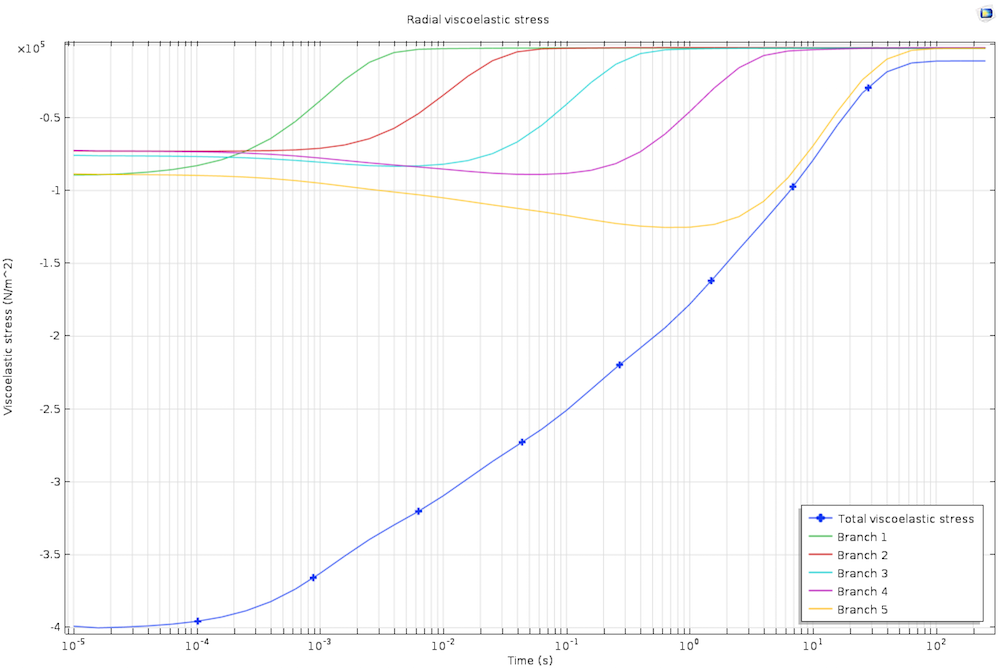
粘弹性分支中的应力。请注意，广义麦克斯韦粘弹性材料的五个分支中的应力的不同松弛时间。

轴向应力比最高的松弛时间放松稳定性更长的时间。在COMSOL多物理学中建模大型粘弹性的能力使我们能够轻松研究和理解不同的生物医学材料和应用。

下一步

• 自己尝试：下载动脉壁粘弹性教程模型和相关信息
• 查看如何使用线性粘弹性减少结构阻尼器的振动

参考

1. G. Holzapfel，非线性固体力学：工程连续方法，约翰·威利（John Wiley＆Sons），2000年。
2. G. Holzapfel，T。Gasser和R. Ogden，“一种用于动脉壁力学的新构成框架和对材料模型的比较研究，”J.弹性，卷。61，第1-48页，2000年。
3. G. Holzapfel，T。Gasser和M. Stadler，“动脉壁粘弹性行为的结构模型：连续公式和有限元分析”，欧洲力学杂志，第21卷，第441–463页，2002年。