
作为我们的一部分求解器博客系列我们已经讨论了解决非线性静态有限元问题,用于改善非线性问题收敛性的负载渐变以及用于改善非线性问题收敛性的非线性渐变。我们还引入了线性静态问题的网格划分考虑,以及如何识别奇异性以及在网格划分时该如何处理它们。在这些主题的基础上,我们现在将讨论如何准备网格以有效地解决非线性有限元问题。
线性和非线性静态问题的回顾
您应该从博客文章中回忆起三个关键点网格划分的注意事项线性静态问题。这些是:
- 线性静态有限元问题总是会在一个牛顿 - 拉夫森迭代中收敛,而不论网格尺寸如何。
- 您应该始终从尽可能粗糙的网格开始,然后手动完善网格或使用自适应网状细化解决更精细的网格。
- 应始终进行网格完善研究,以评估结果的准确性,同时监测收敛远离模型中的任何奇异性。
解决时非线性问题,我们已经了解到,即使是具有单一自由度的有限元问题,即使是有解决方案的问题,也可能不会融合。我们已经学到了几种可以解决此问题的技术,但尚未引入网格和非线性求解器的相互作用。
网络非线性问题
当网格划分非线性问题时要记住的最重要的事情是:
即使问题得到充分,即使我们选择了一种良好的解决方案方法,如果问题在强大的非线性区域中不够细微地分解,问题仍然可能无法收敛。
要理解这一点,让我们看一下一维的热限制元件问题。我们将考虑一个1 m厚的壁,固定温度t = 0一端t = 100在另一个,如下所示:
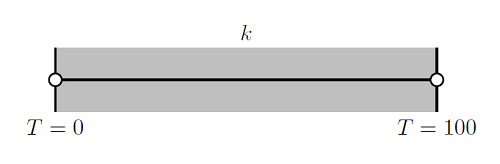
我们将研究该问题的解决方案,以了解下面绘制的不同导电率:
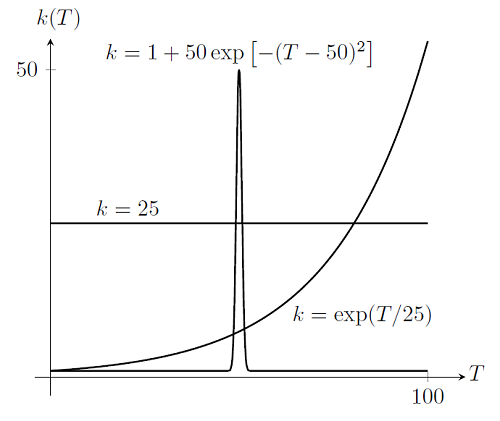
如果我们绘制线性情况的解决方案,k = 25,我们得到:

通过检查,我们看到解决方案是一条直线。对于这种情况,可以通过在整个域中使用单个线性元素找到解决方案。
现在,如果我们策划了案件k = \ exp(t/25),随着元素用虚线描绘,我们得到了:
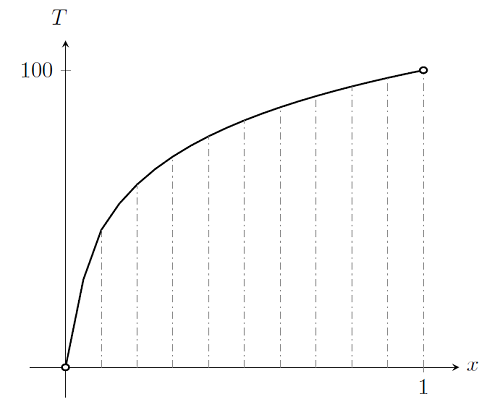
我们可以看到,该非线性问题的解决方案将需要整个域上的一个元素。实际上,无论我们使用多少元素,多项式基函数将永远不会完全匹配真实的解决方案。就像我们为线性问题所做的那样,我们可以依次完善域中各处的网格,并越来越接近真正的解决方案。
最后,如果我们策划了案件k = 1+50 \ exp \ left [ - (t-50)^2 \ right],我们得到:
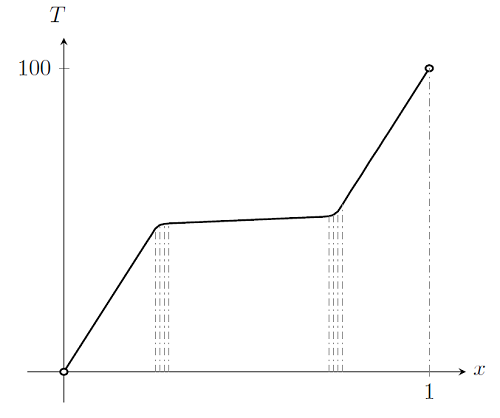
该解决方案更为复杂。清楚地有解决方案的区域,其中单个元素几乎足以完全描述解决方案。然而,在某些区域,该解决方案随着位置的函数而迅速变化。这些区域在附近t = 50,材料属性函数中存在强大的非线性。虽然材料属性功能仅具有一相对于温度强的非线性区域,溶液表现出二该域上的区域迅速变化。只有太空中的这些区域才需要更好的网格。实际上,如果这些区域中的网格太粗糙,则求解器可能根本不会收敛。
对于这些类型的问题,自适应网格的精炼变得高度动机,因为建模域中梯度的位置通常不知道。模型中非线性的渐变也很有帮助,因为从线性问题开始将导致问题始终可以解决,而不论网格如何。通过逐渐提高非线性并进行自适应网格的改进,可以改善非线性问题的模型收敛性。
概括
非线性固定有限元问题的网络与获得非线性模型收敛的问题固有地联系在一起。收敛速率,甚至收敛的可能性都取决于所使用的求解器算法和网格。到目前为止,所有提到的技术:手动和自适应网格的精致,选择初始条件,负载渐变,非线性升值以及这些技术的任何组合可能是您开发越来越复杂的模型的。最后,请务必记住,需要进行网状精炼研究来评估解决方案的准确性。
对于结合了我们到目前为止所学的所有技术的示例模型,请参阅金属的冷却和固化模型。掌握这些技术将使您能够快速有效地对非线性问题进行建模。




评论(0)