平面应力和平面应变有什么区别？

我们生活在一个三维世界中，或者如果您考虑时空的话，我们生活在四维世界中。尽管如此，在工程分析中，通常使用2D近似值来节省建模和计算资源。在这篇博客文章中，我们介绍了使用2D公式在固体力学领域中研究问题的何时以及如何进行。

什么是2D？

现实生活中没有太多实际上是二维的。例如，当我们研究2D电缆横截面周围的电磁场时，我们实际上是在说：“该电缆是笔直的。远离末端的足够远，场仅取决于该横截面平面中的位置。”对于大多数物理问题，这就是想法：在2D近似中，我们研究了一个长而直的对象的横截面，忽略了最终效果。

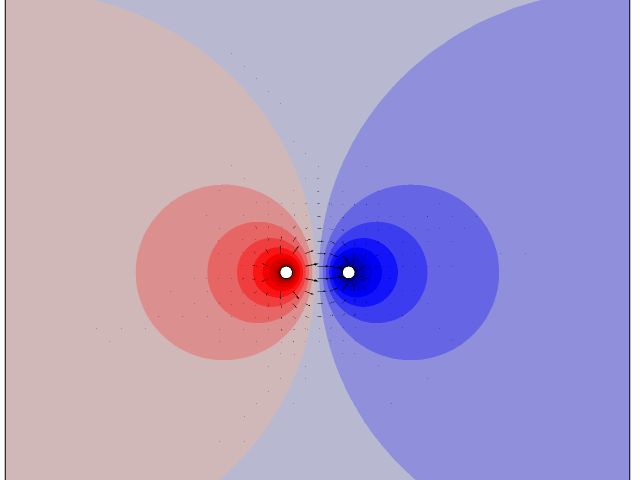
在2D中计算的两条具有不同电位的长电缆周围的电势（颜色代码）和电场（箭头）。

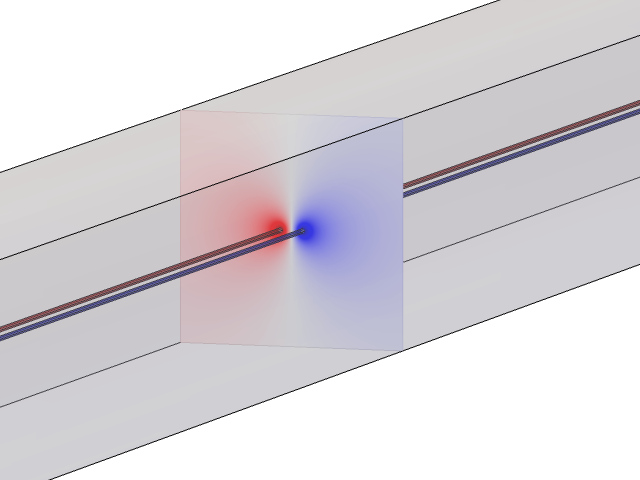
横截面代表了电缆长，笔直和平行的情况。

为什么固体力学特别？

在固体力学领域，2D状态的可能性要多于很长的挤压。例如，我们可以将仅在其平面上加载的薄板板考虑为二维。那是什么使这是可能的固体机制如此特别的？

考虑分析同一板以进行传热。在这种情况下，从大表面的对流和辐射将在平面外向发生。然后，厚度方向的温度梯度很重要。因此，在薄板中进行传热的2D近似更加困难。类似的推理可以应用于许多其他物理现象。

在固体力学的情况下，在平面外方向上也有效果。通常，薄板将在横向方向上变形。例如，如果您伸展它，它将变得更薄。但是，这不会直接影响2D问题的解决方案。厚度变化是可以计算的结果后验，如果您有兴趣。这将在下面更详细地讨论。

固体力学的不同2D公式

在下一节中，假定2D表示xy- 平面，那z是平面方向。位移xy- 平面称为你和v分别是w是位移z方向。

应该注意的是，如果平面内部和平面外动作之间没有耦合（例如，当泊松的比率对于线性弹性材料为零时），则所有配方都是相同的。

平面应变

平面应变是不包含近似值的2D固体力学制剂中唯一的一种。平面应变状态将存在于受约束的对象中z两个刚性墙之间的方向。这也是在概念上具有与其他物理领域中2D公式的最佳对应的公式。但是，对象确实不必在z方向。这与大多数其他物理领域的2D近似值是一个基本差异。

假设很简单：在z方向。

这可以等效地用菌株来表达：

请注意，为了完全避免最终效果，实际上假定刚性壁上的边界条件是滚筒类型的，因此xy- 平面不受抑制。如果不是这种情况，那么我们又回到了我们研究一个远面物体的情况下，远离末端。

平面应力

在平面应力公式中，假设是三个应力张量成分与z方向为零。对于薄板来说，这是一个很好的近似值，但是只有当厚度接近零时，它才完全正确。

在自由表面上，平面应力的局部状态总是占上风，因为这正是边界条件。这就是为什么平面应力假设效果很好的原因 - 在板的两个相对侧是正确的，只要厚度很小，就不明显z方向应力将在内部发展。

广义平面应变

不幸的是，没有对广义平面应变的独特定义，但这通常意味着普通平面应变公式的某些假设是放松的。假设整个应变张量允许非零，但仍然仅取决于X和y。然后，可以证明以下位移场给出了这种应变张量：

这里，A，，，，b， 和C是常数。然后，无限的平面外应变将是

在里面z= 0平面，进行分析，w为零。因此，位移字段中仍然只有两个组成部分，你和v，要解决。但是，有三个新的未知数，A，，，，b， 和C。在对广义平面应变的共同解释中，仅系数C用来。从物理上讲，这意味着允许长对象在z方向。如果参数A和b还包括，挤出还可以以恒定的曲率弯曲。值A，，，，b， 和C由以下假设确定，即没有净轴向力或弯矩在横截面上作用；也就是说，末端是免费的。

当您在comsol多物理学中选择广义平面应变选项时，您可以在纯轴向扩展假设和弯曲的包含之间进行选择。

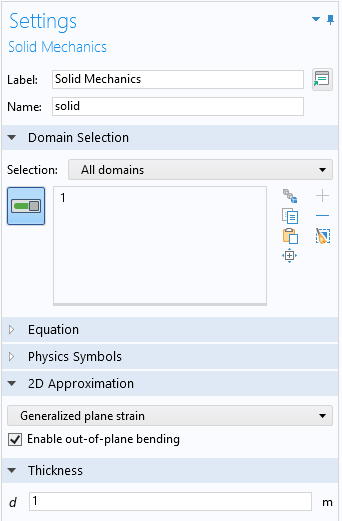
选择广义平面应变。

还有其他有时称为广义平面应变的制剂。例如，平面外剪切应变，\ varepsilon_ {xz}和\ varepsilon_ {yz}，可以允许非零。这样的公式\ varepsilon_ {zz} = 0，在2D版本中使用弹性波，时间显式界面。

构成模型

在线性弹性的假设下，胡克定律可以专门用于平面应变和平面应力。胡克定律的完整3D形式是

这里，e是杨的模量，ν是泊松的比例，而且G是剪切模量。

平面应变

平面应变案例很微不足道；仅需去除从3D公式中零的三个应变组件，

平面应力

对于平面压力案例，事实是\ sigma_z = 0可以用来消除\ varepsilon_ {zz}，给予

然后可以从溶液中计算横向应变（因此厚度变化）\ varepsilon_ {zz} = - \ nu（\ varepsilon_ {xx} + \ varepsilon_ {yy}）。

在ComsolMultiphysics®软件中，不使用此公式。相反，完整的3D胡克定律与一个额外的未知领域一起使用\ varepsilon_ {zz}。当然，这增加了总问题的大小，但是优点是巨大的：无需考虑所有材料模型的特殊平面应力形式，我们不必修改，例如，热膨胀和类似的功能。如果绘制横向应力，\ sigma_ {z}但是，您会注意到该值并非零相同，因为它是使用胡克定律从应变场进行计算的。

广义平面应变

这种情况更加复杂。当在本构之间注入平面外应变的假设时，应力分量显式依赖于坐标。X和y通过系数A，，，，b， 和C。

不可压缩的材料

压缩性程度越小，平面内和平面外动作之间的耦合越强。特别是，许多用于可塑性，蠕变和超弹性的模型都具有不可压缩性。在使用此类材料模型时，所选2D假设的效果特别强。

我应该选择哪种配方？

让我们研究一个简单的矩形板，中间有一个圆形孔。从非常薄的板开始，我们将朝着一个厚的物体移动，在该物体中，孔更像是一条长钻孔的隧道。

平面板尺寸为2 m x 1 m，孔的直径为0.4 m。施加1 MPa的拉伸负荷。使用钢的材料数据。平面应力解决方案如下所示。

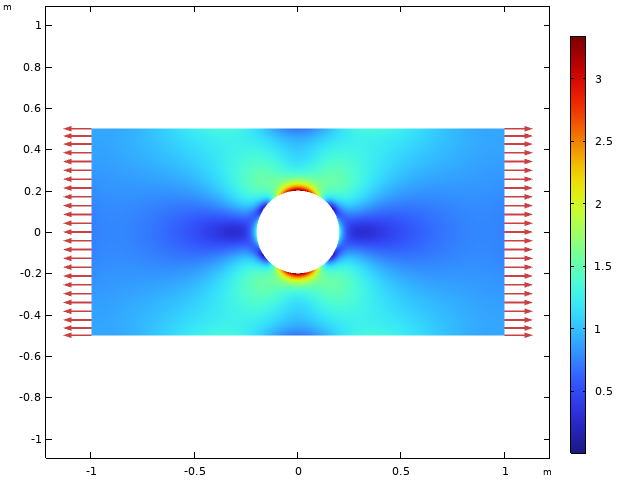
使用平面应力假设，von mises等效应力。

在平面应力假设下，横向应力，\ sigma_ {z}，为零。

接下来，我们转向完整的3D溶液，再次查看同一对象，但分别具有0.1、1和10 m的厚度。在下图中，横向应力，\ sigma_ {z}，被绘制。

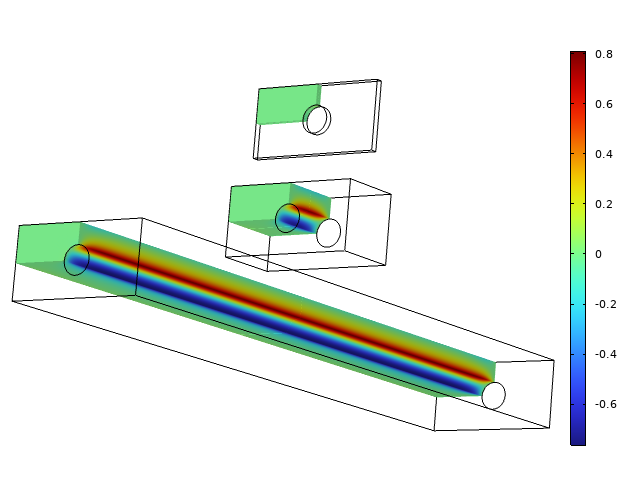
三个不同厚度的横向应力。

对于薄构型而言，横向应力可以忽略不计，因此平面应力是一个很好的假设。对于中间厚度，应力状态是完全三维的。除了长时间，持续的横向应力占上风，除了末端。请注意，最大横向应力为0.8 MPa，因此与施加载荷相比，它绝不可以忽略不计。

在下面，更详细地研究了孔顶部的最压力位置的横向应力。

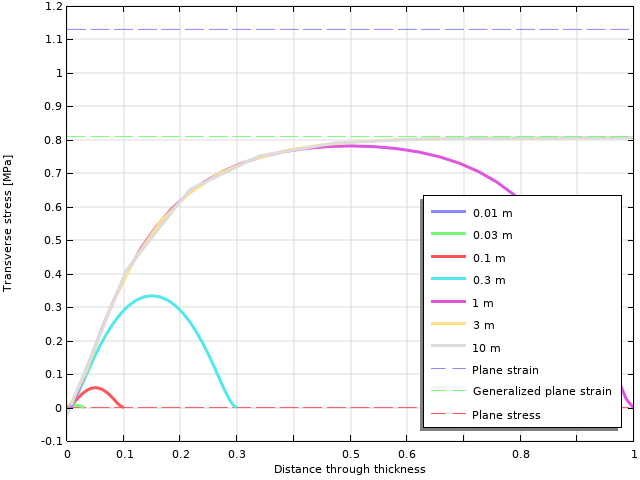
横向应力通过厚度变化。图的参数是对象的厚度。

可以看出，只要厚度为1 m或以上，就可以达到约0.8 MPa的峰值水平。当厚度较小时，最大横向应力会迅速下降。

该图实际上将帮助我们清除两个常见的误解：

1. 仅仅因为一个物体在横向方向上是自由的，并不意味着它处于平面应力状态。
2. 长对象不一定处于平面应变状态。仅当末端被固定时才能保持。

事实是：

• 可以通过平面应力近似具有自由边界的薄物体。
• 一个具有自由边界的长对象可以远离末端，近似广义平面应变。
• 具有与平面尺寸相当的厚度的物体必须被视为完全3D。

实际上，在教科书和在线上，几乎到处都可以发现，应将其厚的物体视为平面应变状态的陈述。虽然在这种情况下，平面应变比平面应力更好，但仍然不正确。广义平面应变假设更好。

我个人的猜测是，由于使用2D解决方案可以追溯到钢笔和纸解决许多问题的时代，例如使用通风应力功能，选择在平面应力和平面应变之间进行实践。使用有限元软件，完整的3D或广义平面应变是较厚物体的更好选择。

为什么会出现横向应力？

在上面的示例中，我们已经看到，即使物体可以自由沿该方向移动，也会在横向方向上发展出明显的压力。为什么？由于泊松的比率效应，平面外方向将发生厚度变化。只要在平面状态下有应力（和应变）梯度，这种厚度的变化不一致。在应力浓度（例如板上的孔中），压力最大的材料希望比周围的材料更薄。相邻的材料将反对这一点，并试图抑制变形。

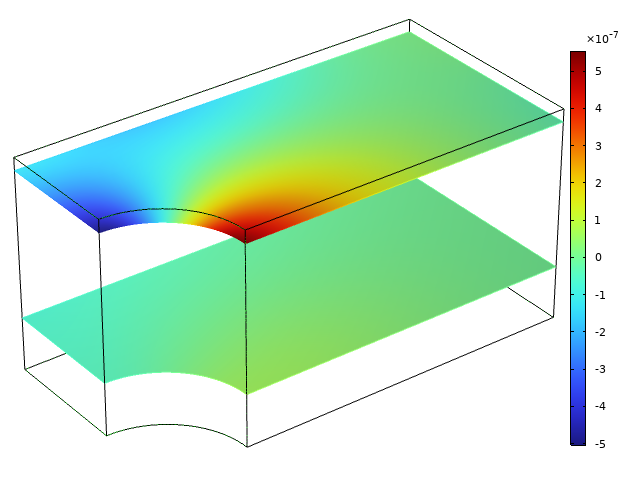
横向位移的变化远离自由表面（底部）和靠近自由表面（顶部）。在每个平面中，平均位移设置为零。

在上一节中，注意到横向应力的大小随距离自由边界的距离而不同。如下图所示，应力分布的细节也与距离自由表面的距离有所不同。

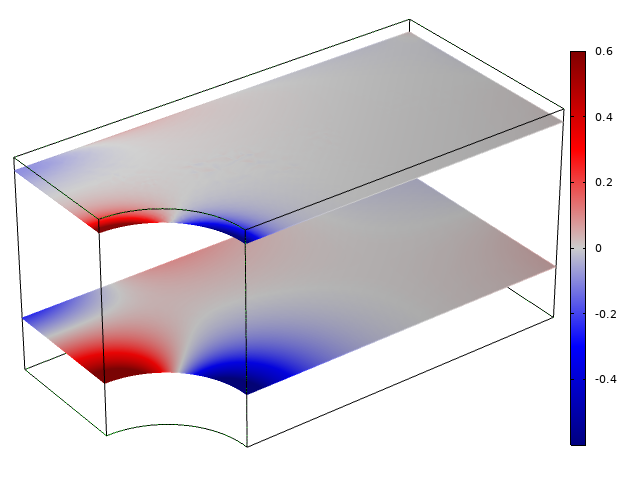
横向应力的分布远离自由表面（底部）和靠近自由表面（顶部）。将应力场缩放为在两个切割平面中具有相同的峰值。实际应力较低，靠近边界。

远离自由表面的横向应力与平面菌株成正比\ varepsilon_x+\ varepsilon_y。由于周围材料的约束效果，整个部分的厚度或多或少均匀。然而，靠近自由表面，横向应力相反，在平面菌株中有较大的梯度的情况下。在这种情况下，靠近孔的边缘。

面内应力呢？

只要该结构仅由街道加载（而不是规定的位移），那么平面应力状态至少与2D假设无关，至少对于线性弹性。但是，这不是完整的故事。在下图中X方向应力显示在孔顶部的压力最强的位置。

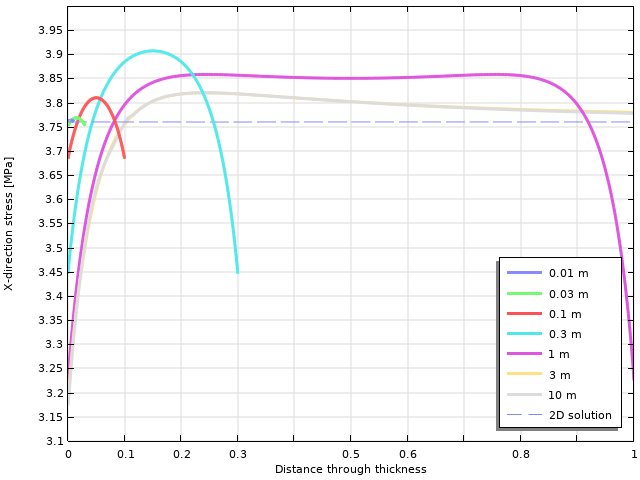
通过厚度的水平应力变化。图的参数是对象的厚度。

可以看出，通过厚度存在显着变化。对于薄物体，2D值匹配良好，而对于较厚的物体，尤其是在自由表面上存在显着差异。这也对等效应力有影响。

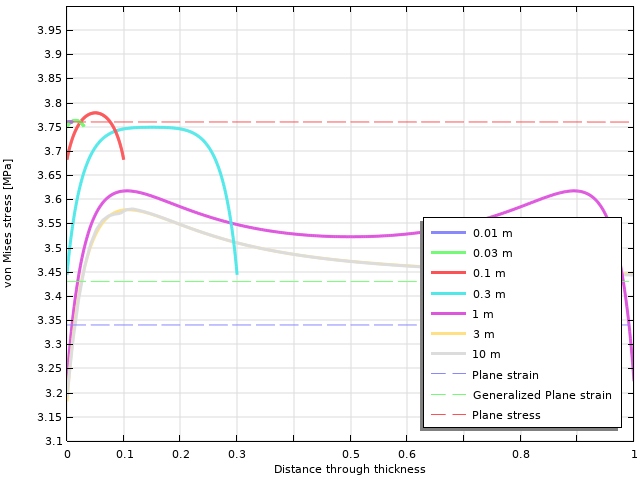
通过厚度的von mises等效应力变化。图的参数是对象的厚度。

对于较厚的物体，实际等效应力与2D溶液中的任何一个之间存在显着差异。只有在相当厚的物体的内部，冯·米塞斯（Von Mises）的应力才会趋向广义平面应变溶液。

非弹性应变

在许多情况下，这三个公式之间的差异并不像上一个示例中的明显差异，而存在重大应力浓度。但是，在某些情况下，您必须特别观察到：当非弹性菌株很重要时。然后，不仅是泊松比对平面菌株的比率效应，在横向方向上起作用。

例如，考虑热膨胀。它通常在各个方向都均匀。这意味着，在平面应变的情况下，在平面外扩展受到抑制，将有很大的横向应力积累。一个可以自由扩展的对象xy- 平面会遇到横向压力\ sigma_z = -e \ alpha \ delta t。如果选择使用平面应力或普遍的平面应变公式，则横向方向的膨胀是免费的，并且不会出现这种应力。

为了说明2D公式在热膨胀情况下的重要性，研究了以下情况：一个方板，具有自由膨胀的平板xy- 平面受到温度与温度成正比的温度场X*y。最大温度升高（在右上角）为100K。使用钢的材料数据。横向上的应力如下图所示。

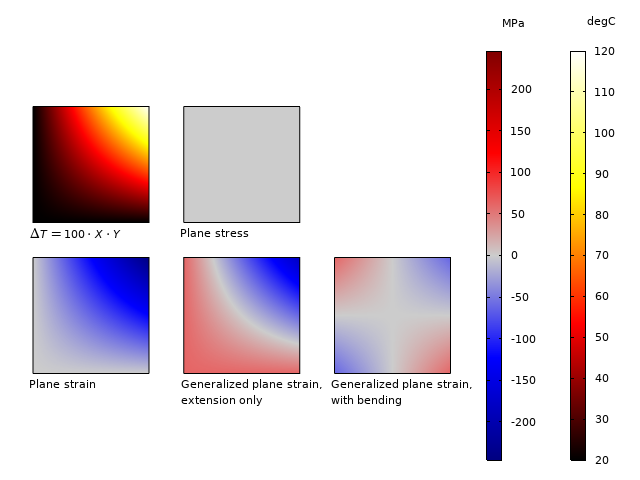
温度分布和面外应力\ sigma_z对于不同的2D假设。

结果表明：

• 对于平面应力案例，平面外扩展是免费的，因此不会诱发应力。
• 对于平面应变，整个部分具有压缩应力，值\ sigma_z = -e \ alpha \ delta t（x，y）。应力范围为-245至0 MPa。
• 对于具有纯伸展的通用平面应变，添加了恒定应力，以便平均\ sigma_z变为零。应力范围为-184至61 MPa。
• 对于弯曲的广义应变，还添加了线性变化的应力场。现在的应力范围为-61至61 MPa。

关于等效应力的注释

两种最常用的标量应力度量是von Mises等效应力和TRESCA等效应力。如果我们根据主要压力来表达它们（\ sigma_1> \ sigma_2> \ sigma_3）， 然后

和

可以看出，中间主应力会影响von Mises等效应力，但不影响TRESCA等效应力。对于2D情况，平面外应力分量\ sigma_z始终是主要压力之一。对于平面应力案例，为零。对于平面应变情况，它是\ sigma_z = \ nu \ left（\ sigma_x + \ sigma_y \ right）= \ nu \ left（\ sigma_ {1 \ mathrm p} + \ sigma_ {2用于线性弹性材料。最后一个表达式包含两个平面内应力。如果\ sigma_ {1 \ mathrm p}和\ sigma_ {2 \ mathrm p}有不同的迹象\ sigma_z始终是中间主应力，TRESCA等效应力不受平面应力和平面应变之间的变化影响。

由于中间主压力的依赖性，冯·米塞斯等效压力无法看到这种不变的行为。

平面应力和平面应变条件下等效应力值之间的差异。Tresca（上）和冯·米塞斯（Von Mises）（下图）。注意TRESCA情况下的较大黑色区域。

关于断裂力学的注释

在断裂力学中，通常在平面应变的假设下分析厚板。为什么我们已经看到了普遍的平面应变或完整的3D是正确的选择，为什么还可以？

在这种情况下，重要的是裂纹尖端处的状态很重要。裂纹尖端处的应变状态是单数的，因此材料沿厚度方向收缩的趋势很强。这是由周围材料抵抗，形成了厚度方向位移的强限制。因此，靠近裂纹尖端的应力状态类似于平面应变。实际上，平面应变溶液和广义平面应变溶液将给出接近裂纹尖端的相似结果。这并不是说平面应变在平面破裂的身体中到处都是一个良好的近似值。实际上，平面应变解决方案将在某种程度上低估全局变形。在大多数板中，应力梯度很小，平面应力是更好的近似值。

下一步

结构力学模块是Comsol多物理学的附加组件，包括用于建模平面应力和平面应变的专门功能和功能。通过单击下面的按钮来了解有关模块的更多信息：