是否存在电压和地面？

我在大学电气工程课程中学到的一些东西，我真正希望有所不同。概念电压和地面属于这一类别，因为这些术语通常以微妙的方式被滥用。我们将为他们提供一个精确的定义，并从了解电磁学和构建良好的计算模型的角度讨论一些有趣的情况。

教科书示例

首先，让我们考虑一下原始和最简单的电气设备之一：电池。以最简单的形式，可以通过将两块金属粘在橙子中。我们可以在电气设备（例如手电筒）中使用电池。我们在电气工程课程中学到的第一件事是如何绘制电路图，看起来有点像以下内容：

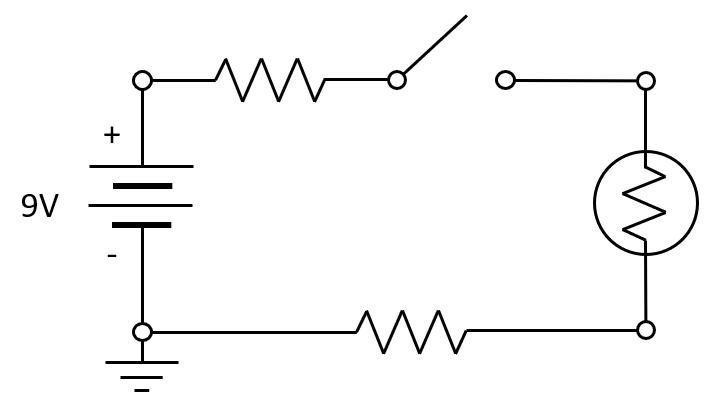
手电筒的基本电路图。

该图显示，我们有一个电池，其中一个端子连接到开关。开关关闭后，电流将流过灯​​泡（发射光），并通过电阻回到另一个电池端子。该设备在DC（时间不变）条件下运行。电阻代表电池的内部电阻以及连接线的内部电阻。连接这些组件的点称为电路的节点。

我们最有可能在学校进行的练习是通过电路计算电流，以及电压在各种节点。但是在这种情况下，电压到底是什么？电压定义为电路中两个节点之间电势的差异，例如电池的两个节点。但是，请注意，我们还在电池的一个端子上绘制了一个地面，我们还将地面定义为：电势为零的节点。因此，如果给我们9伏电池，我们现在知道其他电池端子的电势，我们可以使用Kirchoff的定律来找出相对于接地节点以及电流的所有其他节点电压。

但是，这应该引起一个问题：为什么我们称之为特定的节点基础？我们这里拥有的电路代表一个手电筒，如果完全隔离其他任何东西，手电筒仍然可以工作。（您可以通过将手电筒扔向空气来验证这一点。）我们称之为地面的网络中到底是什么？这是一个完全任意但非常方便的定义。实际上，我们可以选择电路中的任何其他点作为地面（甚至分配了与零不同的值），并为电流获得了完全相同的解决方案。节点电压只会通过常数而不同。也就是说，如果我们对节点的电势有一个解决方案，\ Mathbf {V} = \ {V_1，V_2，V_3，V_4 \}，理论上可以添加任何不变\ Mathbf {V} = \ {V_1+C，V_2+C，V_3+C，V_4+C \}并且仍然有一个有效的解决方案。

但是，有一个警告。我们正在计算机上解决此问题，计算机以有限的精度算术工作，因此我们不想添加一个非常大的常数，例如10^{16} \大约1/\ Epsilon， 在哪里\ Epsilon是双精度浮点相对准确性，因为这将开始引入数值问题。因此，将模型中的一个任意节点设置为零（地面）不仅是教学方便的，而且是良好的数值建模实践。

当使用有限元方法为一组域内的电流求解时，没有太大的变化。可以将有限元方法视为Kirchoff定律的空间分布形式。也就是说，一个有限元模型本质上只是一个更复杂的电路图，并且要在数字上求解它，我们只需要在建模空间中设置一个任意点即可。

坚持，稍等！您是说基地是任意的，只是出于数字目的而存在？

我已经听到了一些电力工程师在磨牙，因为“地面”一词肯定也具有非常真实的物理意义。我们还将地面定义为地球，我们将接地皮带连接到的脚下的物质大球。我们确切地知道它是什么。这是一件非常身体上的事情。但是从电气建模的角度来看，这意味着什么？

从电气上讲，地球是大量的导电材料，并且（至少出于讨论的目的）具有相对可忽略的电阻。这导致了基础的第二个定义：与我们模型中的潜在分布相比，当电流流过它时，电势的域是在触及我们的模型的域，电势的变化相对可忽略不计。

这个新的定义显然与前一个定义不同，有时人们称这种“地面”为“地面”。还有一个类似的概念“底盘地面”或“框架地面”（想想飞机在天空中飞行或汽车的底盘），但即使只是一个非常大的母线，也可以将其定义为地面。

这里的最大区别是，我们将地面的定义从单点更改为一定数量的空间。对于电流而言，这一卷的空间代表了无限的来源和下沉。也就是说，只要由于电池或发电机而存在的电势差，电子就可以永远流入或流出该地面域。

出于计算建模的目的，我们甚至根本不需要对该地面域进行建模。我们只需要指定建模域接触该域的边界即可。由于我们已经说过我们将假设该域内的电动变化可忽略不计，因此我们可以证明在整个表面上应用统一的电势，并且出于前面描述的数值原因，我们选择了零的电位。现在，我们已经到达了地面的定义，我们可以用于建模直流电气系统：零电势的边界，代表电流的无限源或下沉的域。

接下来，我们将研究这些定义如何影响我们的建模方法。

在comsolMultiphysics®中对电压和地面进行建模

仅考虑一段圆线的一段。我们将假设一端连接到地面，另一端连接到源。

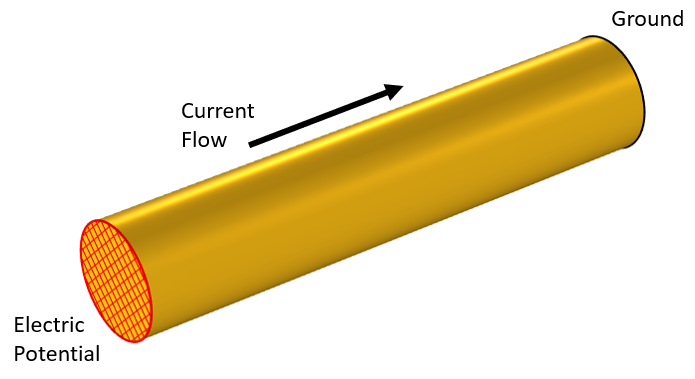
电流电线的一部分模型。

在DC条件下求解电流流程时，我们将这些边界条件的组合在电流界面：

1. 这地面（健康）状况
2. 这电位（健康）状况
3. 这正常电流密度（健康）状况
4. 这终端条件（仅适用于AC/DC模块，MEMS模块，半导体模块或等离子体模块）

这地面和电位几乎是相同的条件。他们固定跨整个表面的电势。这地面条件只需将电位固定为零，而您可以通过电位健康）状况。请记住先前的定义：这些边界代表了一个域的边界，该域是电流的无限接收器（或源），相对于我们的建模域而言，该域内的任何电势差都是可忽略的。如果您要建模连接到电池端子的电线，则这些是适当的边界条件。

第三个选项，正常电流密度，通过表面指定电流通量进入模型。它不会固定电位在整个边界上均匀。一个模型正常电流密度条件通常也有地面条件，所有注入电流的叶子。

一个也可以具有一个有限的有限元模型，该模型具有两个正常电流密度功能，一个注入当前的功能，也可以去除电流。只要这些电流的总和完全为零，就存在解决方案。为了找到此解决方案，添加一个很好的做法是点基由于前面讨论的原因，条件到任何任意点。但是，有趣的是，当以3D建模时，我们实际上可以省略点基完全有条件，只有两个正常电流密度只要它们注入并删除给定有限元网格上的电流完全相同。最终的问题将被取消，但是在3D模型中，我们使用迭代求解器，该求解器将“选择自己的仪表”并仍然汇聚，即使电势场不受限制。有关量规修复的更多详细信息，请参见以前的博客文章“什么是量规修理：理论介绍“ 和 ”如何在comsolMultiphysics®中使用量规修复？“。但是，这一点更像是非常感兴趣的读者的数学好奇心。

最后，终端条件值得单独提及。终端条件具有指定电势的选择，在这种情况下，它在功能上与电位健康）状况。它还可以选择指定总电流。指定电流时，终端条件应用了一个额外的方程式，该方程求解了表面上的电势，从而使所需的总电流流入或流出模型。这终端条件另外会自动计算电阻和其他关注量，因此，如果您具有AC/DC模块或MEMS模块，则通常是首选选项。还有其他选项终端指定电路连接或指定耗散功率或指定与传输线的终止连接的条件，以进行S参数计算。这些更先进的条件在我们的演讲系列中涵盖建模考虑为了电阻和电容设备。

解决模型后，您还需要从中提取数据。通过有限元方法，软件计算字段v（\ mathbf {x}），由此，我们可以提取电场，\ Mathbf {e} = - \ nabla v和当前，\ Mathbf {J} = \ Sigma \ Mathbf {E}，以及这些矢量场中任何一个的大小（规范）。请记住，这些领域将是用网状精炼收敛，除了任何地方模型中的奇异性，您可能或不想解决的问题。

最后，请注意，您可以在模型中两个点之间取出电场的线积分，并且该积分将等于这两个点之间电势的差异。由于我们正在处理标量电位字段，因此该积分是独立的路径：

将电压定义为电场的路径积分的上述方程，一旦我们转化为随时间变化的电磁场的建模，并不总是正确的。这是另一个博客文章的主题，请继续关注！

进一步阅读

• 阅读此博客文章的后续内容：“建模波状电场时的电压和接地“
• 在此处查看此相关学习中心文章：“建模TEM和准TEM传输线“